Էրիկ Վանյան «Մխիթար Սեբաստացի» կրթահամալիր Միջին դպրոց 7․10 դասարան 

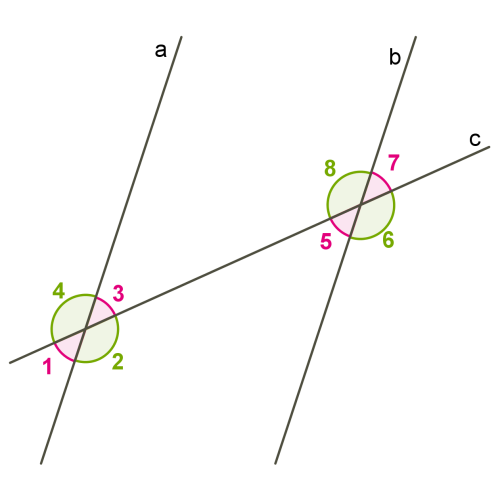
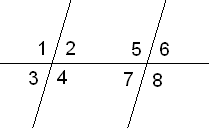
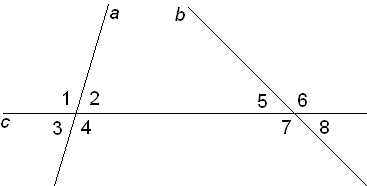
1)Ըստ գծագրի տվյալների՝ գտեք <1-ը։

Քանի որ անկյուններից մեկը 115^o է,իսկ մյուսը 65^o՝65+115=180 

Միակողմանի անկյունների գումարը 180 է,ուրեմն a և b ուղիղները իրար զուգահեռ են։

<1=180^o-121^o=59^o   

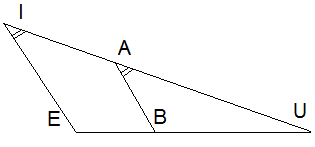
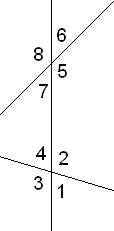
2)Տրված է DE-ն ADF անկյան կիսորդն է։ Ըստ գծագրի տվյալների՝ գտեք ADE եռանկյան անկյունները։

Քանի որ անկյուններից մեկը 78 է,իսկ մյուսը 102,  համապատասխան անկյունների գումարը 180 է՝78+102=180, ապա ուղիղները իրար զուգահեռ են։<ADE=<EDF=(180^o-48^o):2=132:2=66^o 

<A=48^o որպես խաչադիր անկյուններ, <AED=<EDF=66^o որպես խաչադիր անկյուններ։ 

3)Տրված է AB II CD, AB = AC, <BCD=40^o: Գտեք < BAC-ն։

<BCD=<ABC=40^o որպես խաչադիր անկյուններ  

Քանի որ AB=BC ուրեմն հիմքին առընթեր անկյունները իրար հավասար են՝<ABC=<ACB=40^o  

<BAC=180-(40+40)=100 

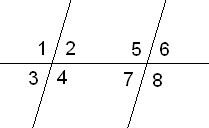
4)Տրված է DE II BC, BD = DE: Գտեք <EBC-ն, եթե <ADE=50⁰ :

Քանի որ <ADE=50^o  <EDB=180-50=130^o

Քանի որ  BD=DE  ուրեմն հիմքին առընթեր անկյունները իրար հավասար են՝<DBE=<DEB,   

<DBE=<DEB=(180-130):2=25^o  <DEB=<EBC=25^o որպես խաչադիր անկյուններ 

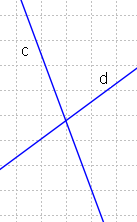
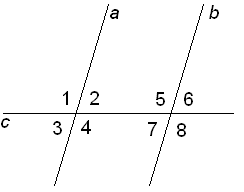
5)Տրված է AB II CD, <BED=80^o , <EDC=30^o: Գտեք <ABC-ն։

<CED=180-80=100^o 

<ECD=180-(30+100)=50^o 

<ABC=<ECD=50^o որպես խաչադիր անկյուններ 

Աքսիոմն այնպիսի ճշմարտություն է, որը չի ապացուցվում: Յուրաքանչյուր գիտություն ունի իր աքսիոմները, որոնց վրա են հիմնվում բոլոր հետագա պնդումներն ու ապացույցները:

Զուգահեռ ուղիղների աքսիոմը.

Տրված ուղղի վրա չգտնվող կետով անցնում է այդ ուղղին զուգահեռ միայն մեկ ուղիղ:

Երբեմն այս աքսիոմն համարում են զուգահեռ ուղիղների հատկություն, սակայն այս աքսիոմի վրա են հիմնված շատ պնդումների ապացույցներ երկրաչափության մեջ:

Զուգահեռ ուղիղների այլ հատկություններ.

1. Եթե երկու ուղիղներ զուգահեռ են երրորդ ուղղին, ապա դրանք զուգահեռ են:

2. Եթե ուղիղը հատում է զուգահեռ ուղիղներից մեկը, ապա այն հատում է նաև երկրորդը:

Առաջադրանքներ․

1)Երկու զուգահեռ ուղիղները հատողով հատելիս խաչադիր անկյունների գումարը 240^o է։ Գտեք այդ անկյունների կից անկյունները։

Քանի որ անկյուն <1+<2=240^o  

Ուրեմն <1=<2=240։2=120^o որպես խաչադիր անկյուններ 

Խաչադիր անկյուններին կից անկյունները հավասար կլինեն՝180-120=60^o

2)Նկարում a, b և c ուղիղները հատած են d հատողով, < 1 = 42 ^o , < 2 = 140^o , < 3 = 138^o : a, b և c ուղիղներից որո՞նք են զուգահեռ։

Եթե երկու ուղղիղներ երրորդով հատվում են և միակողմանի անկյունների գումարը 180^o  է,ապա այդ ուղիղները իրար զուգահեռ են։

<1+<2=42+140=182^o   

a-ն զուգահեռ չի b ուղղին

<1+<3=42+138^o=180^o ուրեմն  a ուղիղը զուգահեռ է c ուղղին։

3)Գտեք բոլոր անկյունները, որոնք առաջանում են երկու՝ a և b զուգահեռ ուղիղները c հատողով հատելիս, եթե՝

ա)անկյուններից մեկը 150⁰ է

<2=<4=150⁰ որպես հակադիր անկյուններ 

<1=<3=180-150=30⁰   

<3=<5=30⁰ որպես խաչադիր անկյուններ  

<5=<8=30⁰ որպես հակադիր անկյուններ

<4=<6=150⁰ որպես խաչադիր անկյուններ  

<6=<7=150⁰  հակադիր անկյուններ 

բ)անկյուններից մեկը 70⁰ -ով մեծ է մյուսից։

Քանի որ անկյունները մեկը մյուսից 70⁰-ով մեծ է,ապա անկյուններից մեկը հավասար կլինի՝180-70=110⁰   110⁰։2=55⁰  

Հետևաբար մյուս անկյունը հավասար կլինի՝180-55⁰=125⁰  

4)Ըստ նկարի տվյալների՝ գտեք <1 -ը։

Քանի որ անկյուններից մեկը 73 է,իսկ մյուսը 107,ապա միակողմանի անկյունների գումարը կլինի 180՝73+107=180,ուրեմն ուղիղները իրար զուգահեռ են,<1=92⁰ որպես համապատասխան անկյուններ 

5)ABC անկյունը 70⁰ է, իսկ BCD անկյունը՝ 110⁰։ AB և CD ուղիղները կարո՞ղ են, արդյոք, լինել՝

ա)զուգահեռ

Այո,որովհետև <ABC+<BCD=70⁰+110⁰=180⁰  

բ)հատվող

Ոչ

Առաջադրանքներ․

1)Ըստ գծագրերի տվյալների պարզել a և b ուղիղները զուգահե՞ռ են:

ա)

a և b ուղղիղները զուգահեռ չեն, որովհետև միակողմանի անկյունների գումարը 180º չէ։

բ)

Այո, որովհետև միակողմանի անկյունների գումարը 180º է։

գ)

Այո,որովհետև միակողմանի անկյունների գումարը հավասար է 180º։

դ)

Այո, որովհետև համապատասխան անկյունները հավասար են։

ե)

Ոչ, որովհետև միակողմանի անկյունների գումարը 180 չէ։

2)Գծագրում m II k, գտնել <1, <2, <3-ը։

<1` 132º, որովհետև անկյունները հակադիր են։

<1=<3=132º,որպես համապատասխան անկյունններ

<3=180-48=132º

<2=<3=132º

3)Գծագրում a II b, գտնել <1, <2, <3-ը։

<1=65º, որովհետև անկյունները խաչադիր են։

<2=180-65=115º որովհետև անկյուները միակողմանի են

<3=<1=65º,որովհետև անկյունները հակադիր են։

4)Տրված է a II b, <1 + <2 = 250^O : Գտնել <3-ը։

<1 =<2, համապատասխան անկյուններ,ուրեմն <2 = 250:2=125º,  <2+<3=180  <3=180-125=55º

Զուգահեռ ուղիղների սահմանումը․

Հարթության վրա գտնվող a և b ուղիղները կոչվում են զուգահեռ, եթե նրանք չեն հատվում: Այդ հանգամանքը նշանակում են այսպես՝ a∥b:

Եթե հարթության վրա գտնվող երկու ուղիղներ ուղղահայաց են նույն ուղղին, ապա դրանք զուգահեռ են:

Հիշենք, մեզ հայտնի հատվող ուղիղների կազմած անկյունների անվանումներն ու հատկությունները:

Հակադիր անկյունները հավասար են՝∡1=∡3,∡2=∡4

Կից անկյունների գումարը 180⁰ է՝∡1+∡2=∡2+∡3=∡3+∡4=∡4+∡1=180⁰

Երկու ուղիղներ երրորդ ուղիղով հատելիս,առաջացած անկյունները կոչվում են այսպես.

Խաչադիր անկյուններ՝∡3 и ∡5;∡2 и ∡8

Համապատասխան անկյուններ՝∡1 и ∡5;∡4 и ∡8;∡2 и ∡6;∡3 и ∡7

Միակողմանի անկյուններ՝∡3и∡8;∡2и∡5

Այս անկյունները կօգնեն ձևակերպել a և b ուղիղների զուգահեռությունը:

Երկու ուղիղների զուգահեռության հայտանիշները․

Հայտանիշ 1.

Եթե երկու ուղիղներ հատողով հատելիս խաչադիր անկյունները հավասար են, ապա ուղիղները զուգահեռ են:

Հայտանիշ 2.

Եթե երկու ուղիղներ հատողով հատելիս համապատասխան անկյունները հավասար են, ապա ուղիղները զուգահեռ են:

Հայտանիշ 3.

Եթե երկու ուղիղներ հատողով հատելիս միակողմանի անկյունների գումարը 180° է, ապա ուղիղները զուգահեռ են:

Առաջադրանքներ․

1)Նշիր նկարին համապատասխան պնդումները:

Այս ուղիղները`

• հատվում են
• զուգահեռ են

2)Եթե հարթության վրա երկու ուղիղներ զուգահեռ են, ապա այդ ուղիղները չեն հատվում:

• ճիշտ է
• սխալ է

3)c ուղիղը հատում է a և b զուգահեռ ուղիղները՝ a∥b:
Գտիր այն պնդումները, որոնք սխալ են:

• Համապատասխան անկյունները հավասար չեն:
• Համապատասխան անկյունների գումարը 180 աստիճան է:
• Միակողմանի անկյունների գումարը 180 աստիճան է:
• Խաչադիր անկյունները հավասար են:
• Միակողմանի անկյունները հավասար են:
• Խաչադիր անկյունների գումարը 180 աստիճան է:

4) Ճիշտ է արդյո՞ք հետևյալ պնդումը`AB∥IE:

• այո
• ոչ

5)Հայտնի է, որ երկու զուգահեռ ուղիղներ հատվում են երրորդ ուղղի կողմից:

Եթե ∢4=138°, ապա∢8=

∢8=∢4=138°    

6)c ուղիղը հատում է a և b ուղիղները: Գտիր այնպիսի անկյուն, որը <4-ի հետ կազմի միակողմանի անկյունների զույգ:

4 և 7

7)Ընտրիր այնպիսի անկյուն, որը <7- ի հետ կազմի խաչադիր անկյունների զույգ:

7 և 2

8)c ուղիղը հատում է a և b զուգահեռ ուղիղները:

Գտիր 2 անկյանը հավասար անկյունները:

<2=<3 որպես հակադիր անկյուններ  

<2=7  որպես խաչադիր անկյուններ

<2=<6 որպես համապատասխան անկյուններ

9)Երկու զուգահեռ ուղիղները հատվում են երրորդ ուղղի կողմից:

Նշիր այն անկյունը կամ անկյունները, որի գումարը <1-ի հետ հավասար է 180 աստիճանի:

<1+<2=180°

<1+<3=180°

Քանի որ,կից անկյունների գումարը  180°  է։

Առաջադրանքներ․

1)A կետի հեռավորությունը շրջանագծի կենտրոնից 7 սմ է, իսկ շրջանագծի շառավիղը՝ 6 սմ։ A կետը պատկանո՞ւմ է այդ շրջանագծին։Գծե՛ք Geogebra ծրագրով և ցույց տվեք։

Ոչ

2)AB և CD հատվածներն O կենտրոնով շրջանագծի տրամագծեր են։ Գտեք AOD եռանկյան պարագիծը, եթե հայտնի է, որ CB=13 սմ, AB=16 սմ։

Եռանկյուն COB=AOD-ին  

Քանի որ շառավիղները իրար հավասար են և <COB=<AOD 

Հետևաբար CB=AD=13 սմ

Տրամագիծը 16 սմ է,ուրեմն շառավիղը հավասար կլինի 8 սմ։

P (AOD)=8+8+13=29 սմ

3)A և B կետերը O կենտրոնով շրջանագծի վրա են։Ինչպիսի՞ն է AOB եռանկյունը։Գծե՛ք Geogebra ծրագրով և ցույց տվեք։

AOB-ն հավասարասրուն եռանկյուն է,քանի որ OA և OB շրջանագծի շառավիղներն են և իրար հավասար են։

4)A և B կետերը O կենտրոնով շրջանագծի վրա են։ Գտեք OAB անկյունը, եթե OBA անկյունը 36^o է։

AOB եռանկյունը հավասարասրուն է, քանի որ OA և OB շրջանագծի շառավիղներն են և հավասար են իրար։

Հետևաբար <OAB=<OBA=36^o 

5)Շրջանագծի շառավիղը 7,1 սմ է։ Գտեք այդ շրջանագծի տրամագիծը։

7,1+7,1=14,2 սմ

Առաջադրանքներ․

1.Հաշվի՛ր CA -ն, եթե CD=8 սմ և ∢AOD=120°

Քանի որ <AOD=120° <AOC=180-<AOD=180-120=60°   OC=OA  Հետևաբար AOC հավասարասրուն եռանկյուն է

<A=<C=60°

Եռանկյուն AOC հավասարակողմ եռանկյուն է՝OC=CA=AO   CO=OD=CD/2=8:2=4 սմ

CA=CO=4 սմ

2. Տրված են շրջանագիծ և մի քանի հատվածներ: Որո՞նք են դրանցից հանդիսանում շառավիղներ, լարեր և տրամագծեր:

Շառավիղներ-AN,AE,AB,AC,AD

Լարեր-FC,NB,CD

Տրամագծեր-NB,CD,

3. Ընտրի՛ր շրջանագծի լարը:

Կարող են լինել մի քանի ճիշտ պատասխաններ:

KL,NM,NK,

4. Ո՞ր հատվածներն են հանդիսանում շրջանագծի տրամագիծ:

HF,KG

5. Տրված է՝ MN=7սմ, ∢ONM=60°։Գտի՛ր՝ KN-ը։

NO և MO շրջանագծի  շառավիղներն են

Հետևաբար NO=MO,եռանկյուն NOM հավասարասրուն եռանկյուն է,<ONM=<OMN=60° <NOM=<ONM=<OMN=60°

Հետևաբար NMO-ն հավասարակողմ եռանկյուն է՝MN=NO=OM=7 սմ  NO=KO=7 սմ

KN=NO+KO=7+7=14 սմ

Լրացրե՛ք բաց թողնվածը.

1)Միևնույն ուղղի վրա չգտնվող երեք կետերով և դրանք միացնող հատվածներով  կազմված պատկերը կոչվում է եռակյուն:

2)Եռանկյունների հավասարության I հայտանիշը — «Եթե մի եռանկյան երկու կողմը և դրանցով կազմված անկյունը համապատասխանաբար հավասար են մյուս եռանկյան երկու կողմերին և դրանցով կազմված անկյանը, ապա այդպիսի եռանկյունները հավասար են»:

3)Եռանկյան անկյան կիսորդի այն հատվածը, որը միացնում է եռանկյան գագաթը հանդիպակաց կողմի վրա գտնվող կետի հետ,կոչվում է եռանկյան կիսորդ:

4)Հավասարասրուն եռանկյան հիմքին առընթեր անկյունները հավասար են:

5)Եռանկյունների հավասարության II հայտանիշ: Եթե մի եռանկյան կողմն ու նրան առընթեր երկու անկյունները  համապատասխանաբար հավասար են մյուս եռանկյան կողմին և նրան առընթեր երկու անկյուններին, ապա այդպիսի եռանկյունները հավասար են:

6)Ըստ գծագրի գտե՛ք x-ը, եթե P=18 սմ, AC=7.5սմ։

AB=BC=X

x+x+7,5=18

2x=18-7,5

2x=10,5

x=10,5:2

x=5,25

7)Եռանկյան պարագիծը 48 սմ է, իսկ կողմերից մեկը 19 սմ: Գտեք եռանկյան մյուս կողմերը, եթե նրանց տարբերությունը 4սմ է:

x+x+4+19=48  2x+23=48   2x=25  x=25:2  x=12,5 սմ  x+4=12,5+4=16,5 սմ

Լրացուցիչ աշխատանք (տանը).

Նոյեմբեր ամսվա մաթեմատիկական ֆլեշմոբ․

Եթե մի եռանկյան երեք կողմերը համապատասխանաբար հավասար են մյուս եռանկյան երեք կողմերին, ապա այդ եռանկյունները հավասար են:

MN=PR

KN=TR

MK=PT

Առաջադրանքներ․

1)

Բերված եռանկյունները հավասար են ըստ՝

III-րդ հայտանիշի

I-ին հայտանիշի

հնարավոր չէ պարզել

II-րդ հայտանիշի

2)Տրված է DCBA ուղղանկյունը: Ըստ եռանկյունների հավասարության երրորդ հայտանիշի, հավասար են արդյո՞ք AOD և AOB եռանկյունները:

AD հավասար չէ AB-ին

Հետևաբար AOD և AOB եռանկյունիները հավասար չեն։

3)Օգտագործելով նկարում բերված տեղեկությունները` գտիր LKN անկյան մեծությունը, եթե ∡LKM=31°-ի:

Ըստ  եռանկյունների հավասարության երրորդ հայտանիշի MKN=LKM

LKM+MKN=31°+31°=62°

Հետևաբար LKN=62°

4)Տրված է, որ VT⊥TU,UT=TS

Գտի՛ր հավասար եռանկյունները:

VT-ն միգնագիծ է և բարձրություն

Հետևաբար ըստ եռանկյունիների երկրորդ հայտանիշի եռանկյունիները հավասար են։

5)Նկարում AB=CD, BD=AC:Հավասա՞ր են ABC և DBC եռանկյունները։

Քանի որ AB=CD  BD=AC 

BC-ն ընդհանուր կողմ է

Ըստ եռանկյունիների երրորդ հայտանիշի եռանկյունիներ ABC-ն և DBC-ն հավասար են։

6)Հավասար պարագծեր ունեցող ABC և A₁B₁C₁ եռանկյուններում AB=A₁B₁ AC=A₁C₁ : Ապացուցեք, որ ΔABC = ΔA₁B₁C₁:

AB=A₁B₁ 

AC=A₁C₁  

Քանի որ պարագծերն հավասար են

Հետևաբար BC=B₁C₁

Ըստ եռանկյունիների երրորդ հայտանիշի ΔABC = ΔA₁B₁C₁:

Եթե մի եռանկյան կողմն ու նրան առընթեր երկու անկյունները համապատասխանաբար հավասար են մյուս եռանկյան կողմին և նրան առընթեր երկու անկյուններին, ապա այդ եռանկյունները հավասար են:

MN=PR

∡N=∡R

∡M=∡P

Առաջադրանքներ․

1)Ապացուցեք, որ եռանկյուն ABC = CDE, եթե <ABC = <CED, BC = CE։

<ACB=<DCE հակադիր անկյուններ

Հետևաբար եռանկյունիներ ACB և CDE հավասար են։

2)ABC եռանկյունում AB = 10սմ, <A = 40^o, <B = 84^o, իսկ MNK եռանկյունում MN = 10սմ,<M = 40^o, <K = 84^o։ Տեղի ունե՞ն եռանկյունների հավասարության երկրորդ հայտանիշի պայմանները ABC և MNK եռանկյունների համար։

Ոչ

3)Նկարում տրված է <DBC = <DAC, BO = AO: Ապացուցեք, որ <C = <D և AC = BD։

<BOD=<AOC  հակադիր անկյուններ

Եռանկյունիներ BOD և AOC իրար հավասար են։

Հետևաբար  AC = BD և <C=<D

Լրացուցիչ աշխատանք (տանը).

1)Նկարում <BAC = <ACD, <BCA = <CAD: Հավասա՞ր են ABC և ADC եռանկյունները։ Պատասխանը հիմնավորեք։

Քանի որ <BAC = <ACD, <BCA = <CAD, իսկ  AC ընդհանուր կողմ է,ապա եռանկյունիներ  ABC և ADC հավասար են։

2)Նկարում AD = A₁D₁, <A = <A₁, <BDC = <B₁D₁C₁։ Ապացուցեք, որ եռանկյուն ABD = A₁B₁D₁:

Քանի որ AD = A₁D₁, <A = <A₁, <BDC = <B₁D₁C₁, հետևաբար  <BDA=<B₁D₁A₁,  ըստ եռանկյունների հավասարության երկրորդ հայտանիշի եռանկյունիներ ABD և A₁B₁D₁ հավասար են իրար։